I explained De Morgan’s Law earlier. In this tutorial, I will solve some problems on this topic. Bubble pushing is another important technique, that should be addressed in this topic.
Learning Objectives:
- Learn more about bubble pushing technique with the help of solved examples
I will show step-by-step procedures for bubble logic or bubble pushing. There is a detailed explanation for two examples while the rest are solved directly. With the help of a detailed explanation, you will be able to evaluate directly as well.
The bubble-pushing technique is related to De Morgan’s Theorem, which is directly applied to circuits containing NAND or NOR gates. Bubble pushing is a graphical technique used in digital logic design to simplify and manipulate logic circuits. The “bubbles” represent NOT gates or negations in Boolean logic. The basic idea is to “push” the bubbles (negations) through the logic gates to simplify the circuit while maintaining the same logic function.
Bubble Pushing Rules:
- When a bubble (NOT gate) is pushed through an AND gate, it becomes an OR gate with bubbles on the inputs.
- When a bubble is pushed through an OR gate, it becomes an AND gate with bubbles on the inputs.
- A bubble on both the input and output of a gate cancels out (Double Negation Law: ¬(¬A) = A).



Solved Examples On Bubble-Pushing:
There are some useful tips to follow while solving these problems.
- Break the longest bar first
- Don’t break the two bars at the same time
- After the bar breaks, change the operator (“+” to “.” and “.” to “+”) underneath the bar.
Example 1: \(\overline{A+B}\)

Example 2: \(\overline{\bar A. B}\)
\(=A+\bar B \text{ Rule 9} \)

Example 3: \(\overline {A+B+C} \)
\(=\bar A . \bar B. \bar C\)

Example 4: \(\overline {A.B.C} \)
\(= \bar A + \bar B + \bar C \)

Example 5: \(\overline{(B+C)A}\)
\(= \bar A + \overline {(B + C)}\)
\(= \bar A + ( \bar B . \bar C)\)

Example 6: \(AB+CD\)
\(\overline {\overline{AB+CD} }\)
\(\overline {\overline{AB}.\overline{CD} }\)
\(\overline{(\bar A+\bar B).(\bar C + \bar D)}\)

Example 7: \(\overline{(A+\bar B)(\bar C+D)}\)
\[=\overline{(A+\bar B)(\bar C+D)}\]\[=\overline{(A+\bar B)}.\overline{(\bar C+D)}\]\[=\bar A. \overline{\bar B} + \overline{\bar C}.D\]\[=\bar A.B + C.\bar D\]

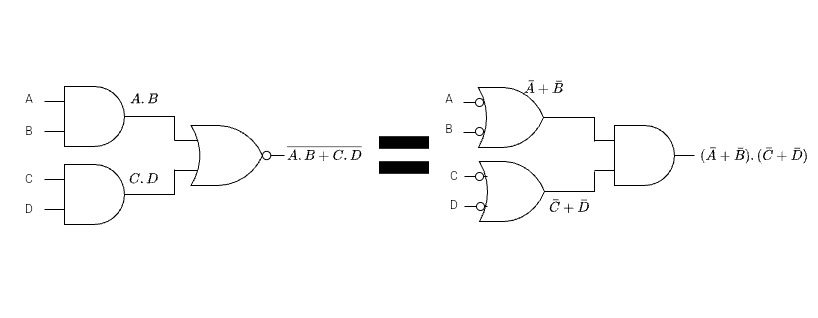
Example 8:\(\overline{A.B+C.D}\)
\(=overline{AB} . overline{CD}\)
\(=(bar A + bar B).(bar C + bar D)\)