The conversion method between hexadecimal and decimal numbers is the same as the conversion method between octal and decimal numbers. I tried to make the explanation as easy as possible. I provide 2 tables, one for calculated powers of 16 and the other for hexadecimal numbers equivalent to decimal numbers.
Key Questions:
- Conversion between decimal and hexadecimal numbers.
- How to convert decimal fractions into hexadecimal fractions.
- How to convert hexadecimal fractions into decimal fractions.
|
164 |
163 |
162 |
161 |
160 |
16-1 |
16-2 |
|---|---|---|---|---|---|---|
|
65536 |
4096 |
256 |
16 |
1 |
0.0625 |
0.0039 |
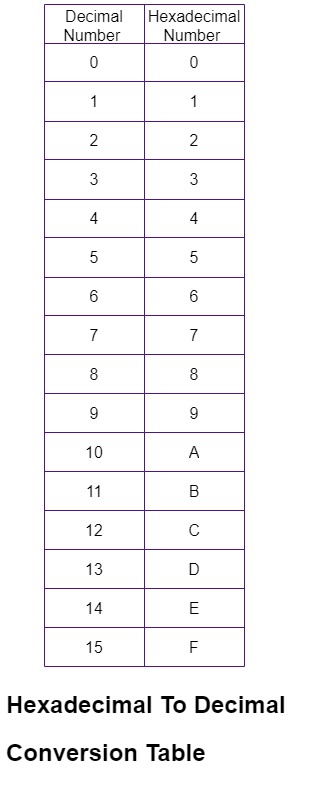
Decimal numbers and their equivalent hexadecimal numbers
Decimal to Hexadecimal Conversion:
As we see in decimal to binary conversion and decimal to octal conversion when converting from a decimal to a binary number system, we use repeated division by 2. If the decimal-to-octal number system, we use repeated division by 8. This time we are working with hexadecimal numbers, so the repeated division by 16 method is used. And if we have a mantissa, or fractional part, then we use repeated multiplication by 16 method. Let’s start with examples.

Example#01:4859)10= ?)16
4859/16 =303 remainder 11)10=B)16
303/16= 18 remainder 15)10=F)16
18/16=1 remainder 2)10=2)16
Look at the highlighted numbers 12FB)16
Answer 4859)10= 12FB)16
Example#02:23456.235)10= ?)16
Solve integer part using division by 16
23456/16=1466 remainder 0 =0)16
1466/16=91 remainder 10)10=)16
91/16=5 reminder 11)10=B)16
Look at the highlighted numbers 5BA0)16
Mantissa will be calculated by using repeated multiplication by 16
0.235*16=3.76 (most significant digit)
0.76*16=12.16)10=C.12)16
0.16*16=2.56. (least significant digit)
0.235)10=0.3C2)16
Answer 23456.235)10= 5BA0.3C2)16
Example#03:1359.79)10= ?)16
For integers, use repeated division by 16
1359/16 =84 remainder 15)10=F)16
84/16= 5 remainder 4
1359)10=54F)16
For mantissa, use repeated multiplication by 16
0.79*16=12.64 = C.64)16
0.64*16=10.24 = A.24)16
0.79)16=0.CA)16
Answer 1359.79)10= 54F.CA)16
Hexadecimal to Decimal Conversion:
As we know, when converting from any number system to a decimal number system, we use the sum of weights method. As for binary numbers, the sum of weights is a power of 2. For octal numbers, the sum of weights is the power of 8. Similarly, for hexadecimal numbers, the sum of weights is a power of 16.
Example#01: 12FB)16= ?)10
12FB)16=(1*163)+(2*162)+(F*161)+(B*160)
=(1*4096)+(2*256)+(15*16)+(11*1)
=4096+512+240+11
=4859)10
Answer 12FB)16= 4859)10
Example#02: 5BA0.3C2)16= ?)10
5BA0.3C2)16=(5*163)+(B*162)+(A*161)+(0*160).(3*16-1)+(C*16-2)+(2*16-3)
=(5*4096)+(11*256)+(10*16)+(0*1).(3*0.0625)+(12*0.00390625) neglect 16-3 which is too small.
=20480+5632+160.+0.1875+0.046875
=23455.23)10
Answer 5BA0.3C2)16= 4859)10
Example#03: 54F.CA)16= ?)10
54F.CA)16= (5*162)+(4*161)+(F*160).(C*16-1)+(A*16-2)
=(5*256)+(4*16)+(15*1).+(12*0.625)+(10*0.0039)
=1280+64+15.75+0.039
=1359.79)10
Answer 54F.CA)16= 1359.79)10

