This topic is a continuation of the number system. I will explain and provide some examples of how to convert from binary to decimal and decimal to binary.
It is a very easy and interesting topic. Anyone can understand easily
Key Questions
- How do I convert binary numbers into decimal numbers?
- How do I convert fractional binary numbers into equivalent decimal numbers?
- How do I convert a decimal to a binary using the sum of weights method?
- How to convert from decimal to binary using the ‘Division by-2’ method?
- Conversions of fractional decimal numbers
| Table for the sum of weights method | |
|---|---|
| 26 | 64 |
| 25 | 32 |
| 24 | 16 |
| 23 | 8 |
| 22 | 4 |
| 21 | 2 |
| 20 | 1 |
| 2-1 | 0.5 |
| 2-2 | 0.25 |
| 2-3 | 0.125 |
| 2-4 | 0.0625 |
| 2-5 | 0.03125 |
| 2-6 | 0.015625 |
Binary to Decimal Conversation:
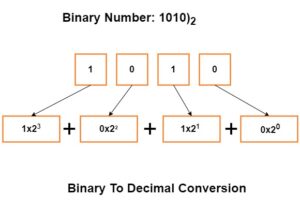
Binary Numbers to decimal number conversion
Multiply each bit by its weight and add all of them.
Example#01: 1001110)2=?)10
1001110)2=(1*26)+(0*25)+(0*24)+(1*23)+(1*22.)+(1*21)+(0*20)
=(1*64)+(0*32)+(0*16)+(1*8)+ (1*4) +(1*2)+(0*1)
=64+0+0+8+4+2
=78)10
Answer 1001110)2=78)10
Example#02: 1101110)2=?)10
1101110)2=(1*26)+(1*25)+(0*24)+(1*23)+(1*22)+(1*21)+(0*20)
=(1*64)+(1*32)+(0*16)+(1*8)+ (1*4)+(1*2)+(0*1)
=64+32+0+8+4+2+0
=110)10
Answer 1101110)2=110)10
Example#03:1011100.01110)2
1011100.01110)2=(1*26)+(0*25)+(1*24)+(1*23)+(1*22)+(0*21)+(0*20).(0*2-1)+(1*2-2)+(1*2-3)+(1*2-4)+(0*2-5)
=(1*64)+(0*32)+(1*16)+(1*8)+(1*4)+(0*2)+(0*1).(0*0.5)+(1*0.25)+(1*0.125)+(1*0.0625)+(0*0.03125)
=64+16+8+4.0.25+0.125+0.0625
Answer 1011100.01110)2=92.4375)10
Example#04:1011001.10101)2=?)10
1011001.10101)2= (1*26)+(0*25)+(1*24)+(1*23)+(0*22)+(0*21)+(1*20).(1*2-1)+(0*2-2)+(1*2-3)+(0*2-4)+(1*2-5)
=(1*64)+(0*32)+(1*16)+(1*8)+(0*4)+(0*2)+(1*1).(1*0.5)+(0*0.25)+(1*0.125)+(1*0.0625)+(1*0.013625)
=64+16+8+1.0.5+0.125+0.013625
= 89.6562)10
Decimal to Binary Conversation:
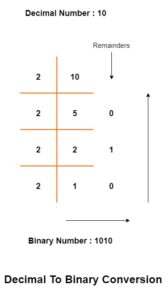
Decimal to binary conversion
There are two different methods of decimal-to-binary conversion.
- The sum of weights method
- Division by 2 methods
The sum of weights method might be confusing. So to avoid confusion and make things clear and easy please refer table above.
Example#01: 78)10=?)2
Division by 2 Method:
78/2=39 remainder 0
39/2=19 remainder 1
19/2=9 remainder 1
9/2=4 remainder 1
4/2=2 remainder 0
2/2=1 remainder 0
Rewrite the bold numbers; start from bottom 1001110)2
The sum of Weights Method:
78 = 64+8+4+2
78 = 26+23+22+21
It can also be written as
=26 +23+22+21
Carefully looking at the above expression. Sum weights that are present.. at the place 6, at the place 3,at place 2 and at the place 1. Assign binary 1 at these places.
The sum of weights that are absent.. at the place 0, at place 4, at the place 5. There is no 20,24,25. Assign binary 0 at these places.
| 26 | 25 | 24 | 23 | 22 | 21 | 20 |
|---|---|---|---|---|---|---|
| Present | Absent | Absent | Present | Present | Present | Absent |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 |
Answer: 78)2=1001110)2
Example#02: 110)10=?)2
Division by 2 Method:
110/2=55 remainder 0
55/2=27 remainder 1
27/2=13 remainder 1
13/2=6 remainder 1
6/2=3 remainder 0
3/2=1 remainder 1
Rewrite the bold numbers, start from bottom 1101110)2
Sum of Weights Method:
110)10=64+32+8+4+2
=26+25+23+22+21
=1101110)2
| 26 | 25 | 24 | 23 | 22 | 21 | 20 |
|---|---|---|---|---|---|---|
| Present | Present | Absent | Present | Present | Present | Absent |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 |
Example#03: 92.4646)10=?)2
The integer part can either be solved by sum of weights method or division by-2 method. While fractional part will be solved by some other technique.
Integer part will be solved by division by 2 method, while mantissa is solved by repeated multiplication by 2.
Division by 2 Method:
92/2=46 remainder 0
46/2=23 remainder 0
23/2=11 remainder 1
11/2=5 remainder 1
5/2=2 remainder 1
2/2=1 remainder 0
Integer =92)10=1011100)2
Mantissa =0.4646
Mantissa will be solved by repeated multiplication by 2
Multiply 0.4646 by 2. Again, pick the resultant mantissa and multiply it by 2. Again, pick the mantissa and multiply it by 2. Repeat until the mantissa becomes zero or the desired number of places after the binary point is achieved.
0.4646*2=0.9292 (MSB)
0.9292*2=1.8584
0.8584*2=1.7186
0.7186*2=1.4336
0.4336*2=0.8672 (LSB)
0.4646)10=01110)2
Answer 92.4646)10=1011100.01110)2
Solved by sum of weights method:
92)10=64+16+8+4
=26+24+23+22
=1011100)2
0.4646)10=0.25+0.125+0.0625
=2-2+2-3+2-4
=0.01110)2
| 26 | 25 | 24 | 23 | 22 | 21 | 20 | 2-1 | 2-2 | 2-3 | 2-4 | 2-5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Present | Absent | Present | Present | Absent | Absent | Absent | Present | Absent | Present | Absent | Present |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
Answer 92.4646)10=1011100.01110)2
Example#04: 89.6785)10=?)2
Division by 2 Method:
89/2=44 remainder 1
44/2=22 remainder 0
22/2=11 remainder 0
11/2=5 remainder 1
5/2=2 remainder 1
2/2=1 remainder 0
89)10=1011001)2
Mantissa will be calculated by repeated multiplication by 2:
0.6785*2=1.357 (MSB)
0.357*2=0.714
0.714*2=1.428
0.428*2=0.856
0.856*2=1.712 (LSB)
0.6785)10=0.10101)2
Answer 89.6785)10=1011001.10101)2
Sum of weights method:
Refer table for sum of weights.
89)10=64+16+8+1
=26+24+23+20
=1011001)2
0.6785)10=0.5+0.125+0.03125
=2-1+2-3+2-5
=0.10101)2
| 26 | 25 | 24 | 23 | 22 | 21 | 20 | 2-1 | 2-2 | 2-3 | 2-4 | 2-5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Present | Absent | Present | Present | Absent | Absent | Absent | Present | Absent | Present | Absent | Present |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Answer 89.6785)10=1011001.10101)2
