This is my first post on binary arithmetic. In this post, I will explain the addition of binary numbers with some solved examples.
Key Questions:
- How to perform binary addition?
- How to perform addition on fractional binary numbers
Binary Addition Rules
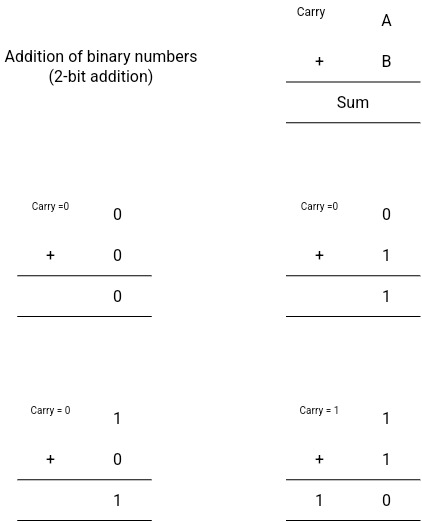
Binary addition is the same as it is in decimal numbers. It’s a simple and easy task. Have a look at the table. Here are some rules for the addition of binary numbers.
| A + B | Result | Carry |
| 0 + 0 | 0 | 0 |
| 0 + 1 | 1 | 0 |
| 1 + 1 | 10 | 1 |
| 10 + 1 | 11 | 1 |
Binary Numbers Addition Solved Examples:
Example # 01: 0101111011)2 + 11111111000)2
| A | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | ||
| B | + | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| Result | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | |
| Carry | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
Check your results:
You can check results by converting each binary number into decimal and add them. I check my results using this online converter.
0101111011)2=379)10
11111111000)2=2040)10
100101110011)2=2419)10
Answer 0101111011)2 + 11111111000)2 = 100101110011)2
Example # 02: 101010111)2 + 1111000011)2
A=101010111
B=1111000011
| A | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | ||
| B | + | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| Result | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| Carry | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
Check your answer:
101010111)2 =343)10
1111000011)2 = 963)10
10100011010)2=1306)10
Answer: 101010111)2 + 1111000011)2 = 10100011010)2
Example # 03: 100111.1100)2 + 111011.1011)2
A=100111.1100
B=111011.1011
| A | 1 | 0 | 0 | 1 | 1 | 1 | . | 1 | 1 | 0 | 0 | |
| B | + | 1 | 1 | 1 | 0 | 1 | 1 | . | 1 | 0 | 1 | 1 |
| Result | 1 | 1 | 0 | 0 | 0 | 1 | 1 | . | 0 | 1 | 1 | 1 |
| Carry | 1 | 1 | 1 | 1 | 1 | 1 | . | 1 | 0 | 0 | 0 |
Check your answer:
100111.1100)2=39.75)10
111011.1011)2=59.6875)10
1100011.0111)2=99.4375)10
Answer:1100011.0111)2
Example#04: add four binary numbers 01011101,11110000,11001100,11011110
Add two numbers at a time. add the third number and then the fourth number.
A=01011101
B=11110000
C=11001100
D=11011110
Step 1:
| A | 1 | 0 | 1 | 1 | 1 | 0 | 1 | ||
| B | + | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| Result 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| Carry | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Check your results:
01011101 = 93)10
11110000 = 240)10
101001101 = 333)10
Step 2:
| Result 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | |
| C | + | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | |
| Result 2 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| Carry | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
Check your results:
101001101 = 333)10
11001100 = 204)10
1000011001 = 537)10
Step 3:
| Result 2 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| D | + | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | |
| Result 3 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| Carry | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
Check your results:
101001101 = 333)10
11001100 = 204)10
1000011001 = 537)10
